LLM Interviews : Vector DBs

I’ll use any resource that helps me to prepare faster.
I’m not directly working for interviews, but preparing for them makes me learn so many stuff, for years(check main page of website for 8 yo youtube channel).
I’ll cite every content I use.
I’ll agressively reference anything I believe explained things better than me.

Vector DBs

Vector DBs

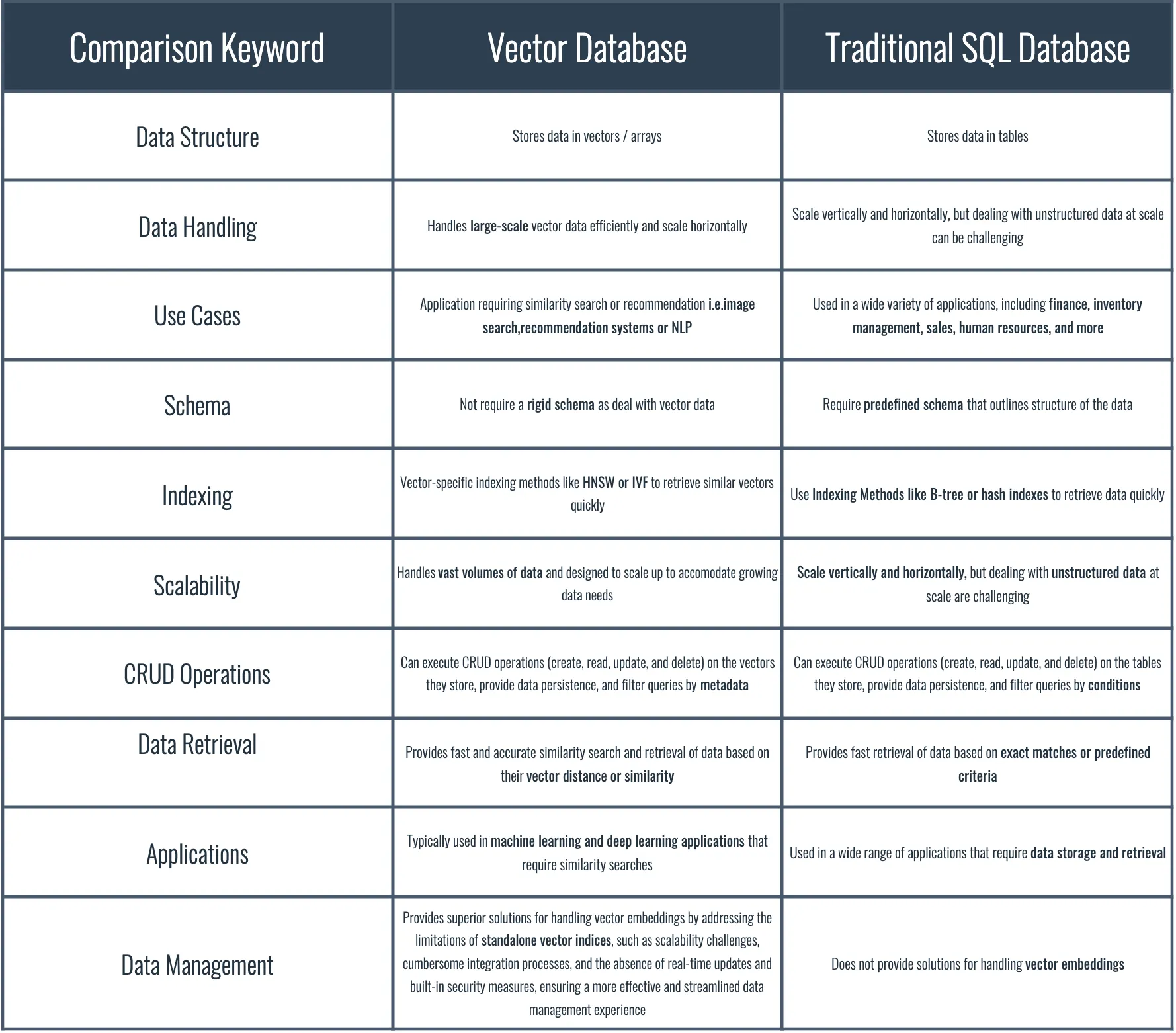
1. What is a vector database? Difference between other DBs.


Resource

2. How does a Vector Database work?

Vector, within the name of the vector database is a representative block of the data. Any data, within its own nature is represented in its own way, does not have to be structured and standardized.

Any method that transforms the unstructured, unstandardized data into standard representation of vector, as simple as [0.12,0.53] can be called embeddings, which allows us to search through the dimensionality reducted/narrow scoped (which is still very structured than the original data) vectors.

Transforming data into vectors require embedding, meaning to transform data into vectors that distinguishes the differences and similarities between the data.

Classical representation after successful embedding below, we see that queen and king is conceptually similar, so they are close to each other. Male and *Female is also a similar concept, so we see that they’re also close to each other.

The reason I tell this is the output successful embedding algorithm is, queen is still closer to woman than male, and vice versa.


Resource

So, successful embedding algorithm:

Preserves Semantic Relationships (of what you desire to have) Similar concepts (e.g., king and queen, man and woman) are placed close together in the embedding space.
Captures Analogical Reasoning (of what you desire to have) It reflects relational patterns such as king - man + woman ≈ queen, showing it understands roles and substitutions.
Maintains Contextual Similarity (of what you desire to have) Words like queen are not only close to king, but also meaningfully closer to woman than to man, showing nuanced understanding.

However the success of model in larger dimensions not really visually observable.

In order to search the DB, it’s obvious we need to find vectors near to what we are looking for. Assume, the below representation is our Vector DB represented in 3D.

So the search term is “dog”

Embed the word “dog”, gives us [1,1,1]
Closer points to [1,1,1], we have wolf [1,1.2,1.2], cat [0.98,1.2,1.2], and more…
We sort those points by closeness to the dog, by calculating distance to the dog, limit the number of data we want to capture.


Resource

We’ll touch to the algorithms later, but k-Nearest Neighbors (KNNs) and Hierarchical navigable small world (HNSW). Also see.

3. What are the vector search strategies?

Assume the question is : You are working on a project that involves a small dataset of customer reviews. Your task is to find similar reviews in the dataset. The priority is to achieve perfect accuracy in finding the most similar reviews, and the speed of the search is not a primary concern. Which search strategy would you choose and why?

Short answer:

Search strategy can be classified into to, one is exhaustive/extensive/exact (whatever it is which means doing full search) k-NN algorithm that calculates distance between all points, rather than approximate nearest neighbors-variant algorithms which are fast but accuracy-decreasing.

1. Exhaustive/Extensive/Exact Search

Method:
Calculate distance between query vectors and searched embedding.

Pros:
%100 Accuracy

Cons:
Slow

2. Graph-Based Methods like HSNW

Method:
See (HNSW). Also see.

Let’s at least discuss this verbally. Imagine the data that we have is below, let’s say this is the all data we have:

0 1 2 3 4 5 6 7 8 9 10

Assume:

0 = snake
1 = gastropot
2 = human
4 = dog
10 = spider

This means that when you go to the right, closer to 10, number of legs increases.

Assume we have an embedding algorithm:

leg_embedder(animal)

that embeds by number of legs.
We want to search "cat" in the db.

leg_embedder(cat) = 4 

In order to find closest animal in our DB, what we need to do is:

search_results = dict()
for animal, leg_value in db:
    distance = leg_embedder(cat) - animal_leg_value
    search_results[animal] = distance

Which requires 11 iterations.
Complexity is O(nd).
And we get %100 accuracy that it is closest to dog.

Graph based method, HSNW, builds some versions (indexes) of the vector DB:

First Layer :     0        5        10
Second Layer:     0   2    5    8   10
Third Layer :     0   2 4  5  7 8   10
nth Layer   :     0 1 2 ..          10 

During the indexings, it is guaranteed that the next layer must include all the vectors/points from the predecessor.

Let’s say if you want to find 3 elements in your search:

First iteration is done on the first layer:
First Layer : 0 *5* 10
Closest distance is 5. Number of close documents we found are 1, we continue.
We move to the second layer, which is more granular:
We look forward to the neighbors of 5, which is 2 and 8.
Calculate distance between 4-8 and 4-2 → 2 is more closer.
Number of close documents we found are 2.
Third Layer:
We go down here and see that the neighbors of 2 are 0 and 4.
Closest to 4 is 4.

Number of documents we found is 3, and we have found [5, 4, 2] as the closest animals.
As it can be seen, with this method we calculated distance 7 times rather than 11.
This escalates quickly with large number of features.

Pros:
Most of the cases, user may not need all documents or the most similar document, doing a batch search could be sufficient. Fast.

Cons:
Decrease in accuracy. Index building can be costly.

3. Tree based Solutions like KD Tree (K-Dimensional Tree)

Examples: KD-Tree, Ball Tree, Annoy (from Spotify). Pros: Good for low-dimensional data. Cons: Perform poorly in high dimensions (>100).

If you have worked with decision trees, limitations will hear you.

Method:
KD Tree is a binary tree used for organizing points in a k-dimensional space. It recursively splits the dataset along one dimension at a time. At each node, it chooses a dimension and splits the data points into two based on a threshold — left if smaller, right if larger.

Pros:

Very fast for low-dimensional data (d <= 20).
Efficient for range and nearest neighbor queries.

Cons:

Performance degrades significantly with high-dimensional data (curse of dimensionality).
Tree building can be slow for large datasets.

Imagine our leg-based animal dataset again:

0 1 2 3 4 5 6 7 8 9 10

And we embed leg_embedder(animal) by number of legs.

We want to search for “cat” with leg_embedder(cat) = 4.

In KD Tree:

We choose a split dimension (say, number of legs).
At the root, we split around a midpoint, say 5.
Everything <5 goes left, ≥5 goes right.

So the tree might look like this:

            5
          /   \
       2         8
      / \       / \
    1   4     6   10

To search:

We start at the root (5), compare 4.
Since 4 < 5, go left.
Then 2: 4 > 2 → go right → reach 4.
Done!

This is faster than checking all points, especially if tree is balanced.

But if our data had 100 dimensions (not just leg count), this splitting becomes meaningless because distances lose meaning — every point becomes roughly equidistant.

4. Tree based Solutions like Ball Tree

Method:
Ball Tree uses a different approach — instead of axis-aligned splits, it creates hyperspheres (“balls”) around clusters of points. Each node contains a centroid and a radius, and all points inside that radius.

Remember the image at the top? Clusters are in blue sphere? Think of like given the query (or the embeddings of cat), we try to place the query to the baloon, then search closests in it.

During search, it computes whether a ball can be ignored based on the query point’s distance to the ball’s boundary.

Pros:

Better than KD Tree in moderately high-dimensional spaces.
Works well when clusters are meaningful.

Cons:

Still not optimal for very high-dimensional data.
Tree construction cost is higher than KD Tree.

Using our same dataset:

0 1 2 3 4 5 6 7 8 9 10

Ball Tree might group:

Ball A: Center 2, Radius 2 → Covers [0,1,2,3,4]
Ball B: Center 8, Radius 2 → Covers [6,7,8,9,10]

Search for "cat" (leg_embedder(cat) = 4):

Compute distance to Ball A’s center: 4-2 = 2 → inside radius → explore.
Ball B’s center is 8 → 4-8 = 4 > radius → skip.

We only need to explore Ball A. Less work than exhaustive search.

5. Tree based Solutions like Annoy (Approximate Nearest Neighbors Oh Yeah)

Method:
If you have used/learned XGBoost, LightGBM, Random Forests, its exactly the same idea. Method gets its power by so many shallow trees. Pros and Cons are also very similar.

Annoy builds multiple trees where each tree is built using random hyperplane projections. At each node, it picks two random points, draws a hyperplane equidistant between them, and splits the data.

During search, it searches across many such trees and aggregates the results.

Pros:

Very fast search after index is built.
Memory-mapped index: works well on disk.
Good for large-scale datasets.

Cons:

Approximate → not guaranteed to return exact nearest neighbor.
Needs multiple trees for good accuracy.
Index size can be large.

Imagine again our dataset:

0 1 2 3 4 5 6 7 8 9 10

Annoy randomly splits data multiple times. For example:

Tree 1:

Picks 1 and 8 → splits at 4.5 → [0–4] left, [5–10] right.

Tree 2:

Picks 0 and 10 → splits at 5 → [0–5] left, [6–10] right.

Each tree gives a slightly different perspective on the space.

To search for "cat" (value 4):

Look in multiple trees.
Each tree returns k-nearest neighbors.
We aggregate results — the most frequent or closest one wins.

This is very fast, since each tree has shallow depth and the splits are random.

But since it’s approximate, sometimes it may miss the true closest match — unless we use many trees and large search k.

Some more source on annoy

6. Hash-Based Solutions Locality Sensitive Hashing

Method:
See

Pros:
Very fast lookup once indexed. Works well in high-dimensional spaces (like embeddings).

Cons:

Approximate — can miss true nearest neighbors. Needs many hash tables for good accuracy. Can consume a lot of memory with large datasets.

4. How does clustering reduce search space? When does it fail and how can we mitigate these failures?

It reduces search space by not trying to find distance on all vectors, but trying to find closest cluster first, then calculating distance on the vectors of closest cluster. Ball-Tree method is a good example for that.
It does fail when:
1. Embedding is poorly chosen.
2. In high dimensions, (means embedding creates [1,100] for query rather than [1,10] let’s say), clustering becomes meaningless and less quality. We may need to reduce dimensionality.

4.1 Estimate RAM/Memory Needs of Such Database (without Any Compression)

Pinecone has a great explaining why do we have indexing methods.

Vector similarity search can require huge amounts of memory. Indexes containing 1M dense vectors (a small dataset in today’s world) will often require several GBs of memory to store. The problem of excessive memory usage is exasperated by high-dimensional data, and with ever-increasing dataset sizes, this can very quickly become unmanageable.

Let’s estimate the Size of 1 Million 1-page pdf DB

Referencing the numbers from here, also mostly used in vector database tutorials, let’s assume we embed with “all-MiniLM-L6-v2”. This model outputs the size of (1,384) float32 array.

Standard A4 page contains 500 words, assume we chunk per half-page. Float32 is 4 bytes. 384 floats per embedding * 4 bytes * 2 chunk per page * 1,000,000 documents = 3 GB.

If we are ok to use float16 precision, which is possible, then it’s only 1.5 GBs.

Or, if you wanna go with “text-embedding-ada-002” from OpenAI because you think search quality is better, it has 1536 float32’s in its vector, with same chunking strategy (although you may want to experiment with chunk size), it would be 15 GBish.

In order to reduce the memory usage and performantly query the DB, we should reduce the size but minimally loss search-retrieval performance. There are ways of it.

5. Explain product quantization (PQ) indexing method?

Again from Pinecone.

Product quantization (PQ) is a popular method for dramatically compressing high-dimensional vectors to use 97% less memory, and for making nearest-neighbor search speeds 5.5x faster in our tests.*

And, although I’ll cite, summarise and use the images from amazing blog of Vyacheslav Efimos, for better understanding please read it.

When I’ve read about PQ, I remembered the days where I was 7-zipping the rar folder I’ve saved game setup to my 1 GB Toshiba USB at 2009.


Resource

As you remember, we embedded with “all-MiniLM-L6-v2” that outputs to a (1, 384) float32 array.

But assume we have an algorithm that embeds to (1, 8) per chunk, in binary values like: [0,1,0,1,1,1,0,1]

This means we can have 2⁸ = 256 possible vectors.

Let’s simplify the LOGIC, not yet the exact algorithm, just the basic idea:

Step 1: Divide the vector into subvectors. Let’s divide the vector into 4 subvectors: [0,1] [0,1] [1,1] [0,1]
Step 2: Assign unique identifiers to each subvector. Instead of storing these subvectors directly, we can represent them with unique integer identifiers:
[0,0] -> 0
[0,1] -> 1
[1,0] -> 2
[1,1] -> 3
Step 3: Embed the vector using the identifiers.

Thus, the vector can be embedded as: “1131”

Where:

1 refers to the second subvector [0,1]
3 refers to the fourth subvector [0,1]

Instead of storing the 256 possible vectors in 8 integers, we now only store them in 4 integers. Even in this small example we reduced to %50.

And during the similarity search,

Step 1: Let’s say we want to query [0,1,0,1,1,1,1,1], it’s 1133.
Step 2: Calculate distance on the PQ values. (1-1)^2+(1-1)^2+(3-3)^2+(3-1)^2=4. So again we find a similar chunk. However, this time we did 4 operations instead of 8.

PQ works similar way, the differences are:

Embedding size is huge like (1, 384) and float, so we cant find exact clusters like [0,1].
Rather we estimate clusters, with cluster algorithms. For each cluster, we assign integer as we do above.
Since clusters are not exact representation of the data we have, it’s a lossy compression. But it’s OK because we try to rank/get least distanced samples with query.

Referencing to Vyacheslav Efimos’s blog,

Imagine an original vector of size 384, which stores floats (32 bits), was divided into n = 8 subvectors
where each subvector is encoded by one of k = 256 clusters.
Therefore, encoding the ID of a single cluster would require log₂(256) = 8 bits.
Let us compare the memory sizes for the vector representation in both cases:
Original vector: 384 * 32 bits = 12,288 bytes.
Encoded vector: 8 * 8 bits = 8 bytes.
The final compression is 1536 times! This is the real power of product quantization.

6. Explain Locality-sensitive hashing (LHS) indexing method?

TBC.

7. Compare different Vector index and given a scenario, which vector index you would use for a project?

TBC.

8. Compare different Vector index and given a scenario, which vector index you would use for a project?

TBC.

9. What are the current Vector DBs known?

Dedicated Vector Databases: Pinecone, Milvus, Qdrant, Weaviate, Chroma, Vespa, Vald, Zilliz, Deep Lake, LanceDB, Marqo, SemaDB.

Vector Search Capabilities in General-Purpose Databases: PostgreSQL with pgvector, MongoDB Atlas, Elasticsearch, OpenSearch, Apache Cassandra, Redis Stack, SingleStoreDB, Oracle Database, MySQL, MariaDB, Supabase, ClickHouse.

Vector Search Libraries: Faiss, ScaNN, Annoy.

Side Notes:

%90 of the blog is/will be written by me.
I may use ChatGPT to create %10 of the blogs, just to make content easier to read/to markdown format the algorithms. But nothing more than this. Just for help.
This doesn’t mean I create posts with ChatGPT, and proof-read and additions. It means I create posts by myself, in the middle I found ChatGPT can graph/format algorithm better than me, and prompt what I want to explain to it. Then it gives better format/fun to read content for just some part of the blog.
The reason is, I already spend time to create content, and I’m learning while writing, but I understand content before writing, so I want to minimize writing time.